The iris-lean project aims to port Iris into Lean. As it stands now, the project is mainly a formalization of Iris Proof Mode frontend MoSeL.

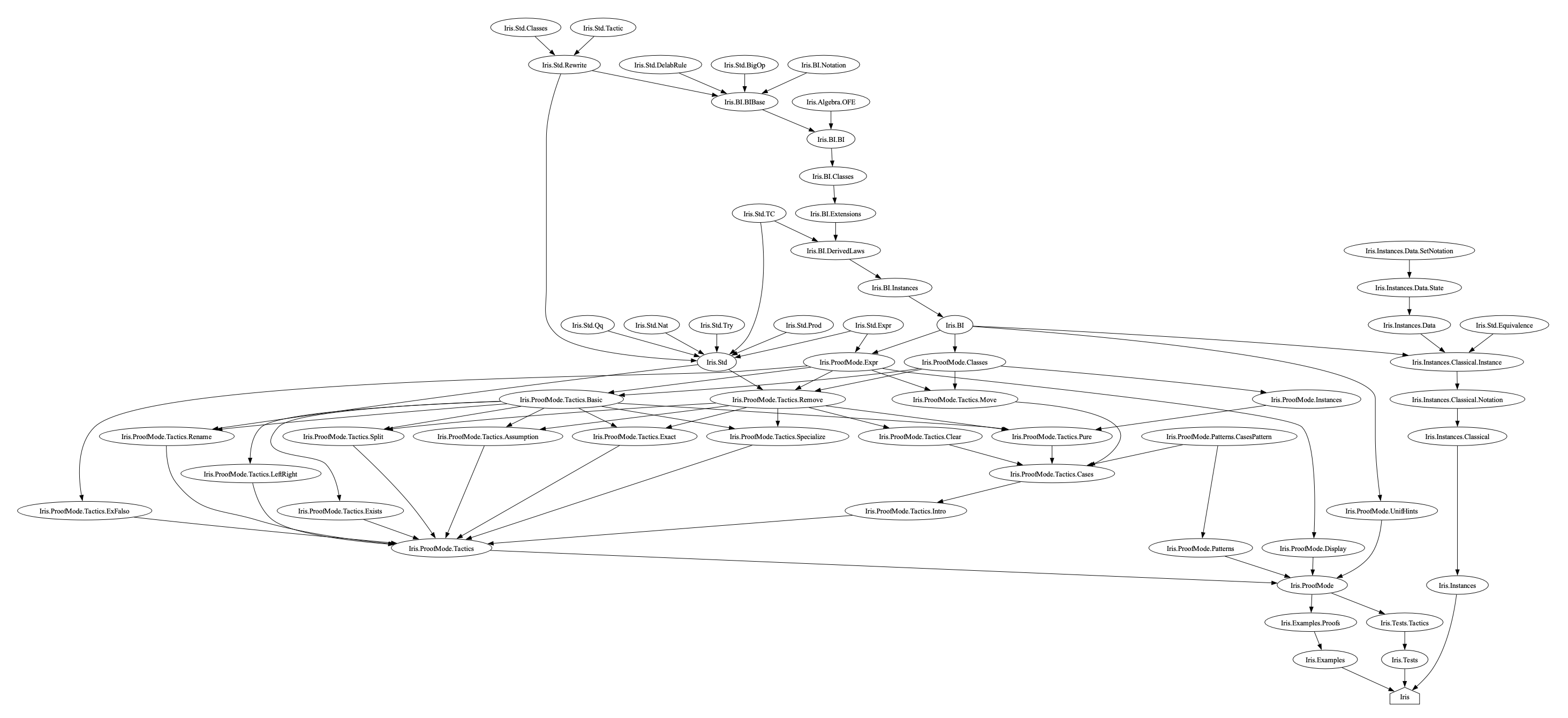
I want to understand concretely what iris-lean has accomplished, in order to judge how it might be used for mechanizing other separation logics in Lean. To do this, I worked my way up the project’s import graph, and made an inventory of which kind of theorems are in each file.

Higher-res version

Notes

Here are my notes about what each file in the iris-lean repository does.

• Iris.Std.Classes
  • Typeclasses for basic properties about binary relations
  • Surely these are in mathlib somewhere
  • Does this relate to generalized rewriting
• Iris.Std.Tactic
  • Basic helper tactics for manipulating goals
  • Seems generally useful
• Iris.Std.Rewrite
  • A more general rewriting tactic “for preorders with monotone rules on how to destruct operators.”
  • Rewrites vary based on how many times they’re performed
  • What is monotonicity in this context?
  • What is the differences between rewriting with monotonicity, and fully generalized rewriting?
• Iris.Std.DelabRule
  • It has one tactic but I’m not sure what it does
• Iris.Std.BigOp
  • “Big Operators” implemented with a left fold, with “unit” as base case
  • LawfulBigOp f unit eq: f is lawful with respect to an equality relation eq
  • Are all Iris BigOps lawful?
• Iris.BI.Notation
  • Notation for iProps?
• Iris.BI.BIBase
  • Typeclass: embedding of a separation logic into PROP : Type
  • Seems to be a subset of the Iris base logic? Where exactly did this come from?
  • Tons of syntax and macros based on BIBase
• Iris.Algebra.OFE
  • Basic definitions for OFE’s, COFE’s, discrete COFE
  • No instances
• Iris.BI.BI
  • Extends both BIBase and COFE
  • Proof rules that must hold about the embedding
  • This typeclass could be split up into a Mathlib-like hierarchy
  • Somehow connects back to rw_mono_rule, registers that attribute for bi_sep_mono and persistently_mono
• Iris.BI.Classes
  • Typeclasses for various kinds of iProps (persistent, affine, absorbing, intuitionistic)
• Iris.BI.Extensions
  • Extension of BI for affine logics
  • Makes me think that BI could be broken up more
• Iris.Std.TC
  • Typeclass combinators
  • I am astonished that there is any use for this
  • class inductive, unif_hint: none of these words are in the bible
• Iris.BI.DerivedLaws
  • Lemmas that follow from the BI typeclass
  • I see “mono” lemmas, connected to rw_mono_rule. Does that mean you can rewrite under them?
  • LawfulBigOp instance for:
    • and with equality BiEntails and unit True
    • sep with equality BiEntails and unit emp
• Iris.BI.Instances
  • Affine, Absorbing, Intuitionistic, and Persistent instances for BI definitions
• Iris.Std.Expr, Iris.Std.Nat, Iris.Std.Prod, Iris.Std.Expr, Iris.Std.Qq, Iris.Std.Equivalence
  • Various helper functions, for both programming and metaprogramming
• Iris.Instances.Data.SetNotation
  • Typeclass for disjointness, and notation (- || -)
• Iris.Instances.Data.State
  • State is a function Nat -> StateResult, and StateResult is either “unknown”, “result -”, or “conflict”
    • I suppose this is their definition of memory for this instance
    • Doesn’t the Iris base logic use a CMRA for this?
  • Disjoint states, “unknown” means outside of a heap fragment
  • Set operations on states
• Iris.Instances.Classical.Instance
  • BI instance (resp. BIBase and discrete COFE) for propositions over State (HeapProp)
  • BIBase is just lifting
    • later does no step-indexing
    • persistently means the proposition is state-irrelevant
• Iris.Instances.Classical.Notation
  • “points to” HeapProp

I didn’t end up reading anything in ProofMode, because Lean metaprogramming is still magical to me, and I’m happy to leave it as “that code works”. There is a single example in the repository.

What does iris-lean do, and what’s next?

iris-lean implements a collection of tactics against a particular axiomatization of separation logic.

The most glaring deficiency in iris-lean is the fact that it’s never actually instantiated. Trying to do this for a simple separation logic (and mechanizing its adequacy theorem) would be an obvious next step. I suspect that in the process of doing this, one would need to break up the BIBase typeclass into smaller components—not every logic will have all of the features of Iris. This could possibly be a fragment of one of the early logics presented in Iris from the Ground Up, but I think that might even be a little much at this point.

They also have no program logics developed on top of their separation logic. Implementing an analogue of the generic program logic code from Iris would probably require a lot of work. It would be nice if there was generic tactic-writing code for this.

The results for OFEs and COFEs could be ported from regular Iris, since those have no dependencies in Iris. I’m curious about if any of this work can integrate into Mathlib.

The README for iris-lean mentions an issue with generalized rewriting. I don’t fully understand how they solve this issue with their rw' tactic in the development. Which features of generalized rewriting does iris-lean need, and what has changed since this project was under development?

Code

My fork is updated to Lean 4.14.0-rc2. The import graph was generated using importGraph.